
Part
1
Fourth
Dimension
At present the term " fourth dimension" is used mostly by science
fiction writers. Some scientists only assume
hypothetic possibility of the fourth and even the fifth and so on
dimensions existing. But there is no authoritative and proved grounds
to
this assumption. It should be noted that speaking about the fourth and
so on dimensions their geometric-spatial version is
supposed. The notion of three dimensions: length, width, height (three
dimensional system of co-ordinates) is an axiom. There is no subject to
be discussed, but! Let's try to make some short analysis.
Point
of departure
a) beginning of co-ordinates
It is infinitesimal point (nought) arranged in any point of
space. It means that we can always dispose it in such a way
that any
body, process can be described in positive. (Mathematics in
physics "doesn't want" to work with negative numbers: mathematics: 2 -
5 = -3, it's O.Key. But in physics 2 bodies - 5 bodies = -3
bodies, it's absurdity).
b) first dimension
It is a straight line, rather a ray, originating from the point
of
the beginning of co-ordinates.(fig.1)
We take arbitrary length of a piece as a unit of measurement, for
example: a meter, an inch, a mile etc. This measurement
determines the length of pieces. Here mathematics is arithmetic.

Fig.1.
c) second dimension
This ray originates from the point of the beginning of co-ordinates
angle-wise 90degrees to the ray of the first
dimension.
(fig.2). We take the same unit of measurement like in the first
dimension, but it's not necessary. We 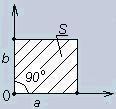
may take FOOT for example, it will be m x foot.
We may also take a unit
of area not in the form of
a square, but in the form of a parallelogram, a
triangle, a
hexagon and so on. It's important to understand that the unit
obtained is independent, non-derivative.
We may know nothing about
the first dimension. But if we take a certain area (a sheet of veneer,
for example); this sheet is an independent example of the
unit. A square meter isn't m x
m in the
least. It can be in the form of a rectangle with
its sides
0,5m and 2m, in the form of a triangle, in this case its
Fig.2
area must be equal to the above
mentioned example. In
general, multiplication of a meter by a meter
is similar to multiplication (or division) of a cow
by a cow. Such units as an
acre,a hectare and so on
should be used . Therefore with the help of the second
dimension
we can describe plane geometric figures and lines and their
mutual disposition in the plane. Mathematics here
is
planimetry and algebra.
d) third dimension
Look
at the
figure.
You have already understood that cubic
measure here can be
in the form of a parallelepiped, a pyramid and so
on
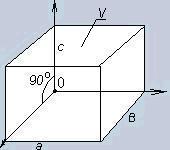 and can be named : a litre,a gallon,
etc. The obtained unit is independent.
With the help of the third dimension we can
describe solid figures, spatial
lines and their
mutual disposition. Here mathematics
is stereometry, algebra,
differential calculation.
and can be named : a litre,a gallon,
etc. The obtained unit is independent.
With the help of the third dimension we can
describe solid figures, spatial
lines and their
mutual disposition. Here mathematics
is stereometry, algebra,
differential calculation.
Fig.3
Here comes the analysis
itself.
It consists in successive comparison of each
dimension with
the previous one and the searching for possible
regularities on this basis. Don't forget that
absolutely
everything equals nought in zero dimension.
1. The
first dimension
(linear) differs from zero dimension so that
when we add it we get the first independent
(non-derivative!) unit - the unit of length, scope
of dimension
from 0 to infinity. This dimension
includes the
previous 0 dimension.
2.The second dimension(plane)
differs from the first one by appearance of a new independent
unit - the unit of area, range of measuring from 0 to
infinity
and this dimension includes all the previous dimensions.
3. In third
dimension(space) a new
independent unit appears again. The unit
of cubic content, range of measuring from 0 to infinity.
This
dimension includes all the previous ones.
Here we have such phenomenon as NEST-DOLLS.
Note:
it's very important to understand every
current unit is
independent. For example: your parents are
John and
Mary, you may be called "the son of John and Mary" but you are a new
independent personality with your own characteristic features. You are
Steve. And your son should be called "the grandson of John
and
Mary plus another grandma, another granddad", and his son should be
called… It's not only because it's inconvenient , but
dealing with
you I deal concretely with Steve, not with
somebody's son.
I appreciate exactly your characteristics, but not the product of
ýour parents'characteristics. The same is with
characteristics
of the unit of area : its characteristics are not
characteristics
of the product of a meter by a meter .
Conclusions:
during the analysis a certain regularity of consistency in dimensions'
construction was revealed:
1. Units of measuring are positive numbers in a
range from a zero to infinity.
2. Each following dimension
includes all the previous ones.
3. Every dimension creates a
new, independent unit of measuring..
The obtained
regularity determines algorithm of consistency in
dimensions' costruction.
4.Fourth dimension.
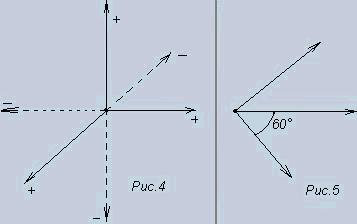 Three
dimensions are depicted in fig.4. In order to construct fourth
dimension one more axis should be drawn. Drawing it
in the
domain of these three dimensions doesn't have any sense. And
drawing it in the domain of negative numbers contradicts to algorithm.
It should be noted that Decart system of
co-ordinates (
axes at angle 90˚ ) isn't a dogma. For example, axes can have 60˚ as it
is shown in fig.5. To draw here the fourth axis seems quite possible .
Please try if you've got time. One needs to understand that
all
the dimensions are abstraction, created by ourselves for
describing something. There is objective reality: space, material
bodies, processes occurring in substance. We
have described space in
three
dimensions, it's time to describe substance.
Three
dimensions are depicted in fig.4. In order to construct fourth
dimension one more axis should be drawn. Drawing it
in the
domain of these three dimensions doesn't have any sense. And
drawing it in the domain of negative numbers contradicts to algorithm.
It should be noted that Decart system of
co-ordinates (
axes at angle 90˚ ) isn't a dogma. For example, axes can have 60˚ as it
is shown in fig.5. To draw here the fourth axis seems quite possible .
Please try if you've got time. One needs to understand that
all
the dimensions are abstraction, created by ourselves for
describing something. There is objective reality: space, material
bodies, processes occurring in substance. We
have described space in
three
dimensions, it's time to describe substance.
Let's put everything in order:
a) First dimension
 Here the unit
is - an agreed piece.
Here the unit
is - an agreed piece.
b) Second dimension
 It can be represented in the form of one axis,
because
this dimension has already included the previous
one. Here
the unit of measure is an agreed
area.
It can be represented in the form of one axis,
because
this dimension has already included the previous
one. Here
the unit of measure is an agreed
area.
c) Third dimension
 It can also be represented
in the form of one axis. Here the unit of measure is an agreed cubic
content.
It can also be represented
in the form of one axis. Here the unit of measure is an agreed cubic
content.
/ The same order is
valid for the following dimensions /
d) Fourth dimension
 In
order to describe substance which is characterised by density, let's
draw a corresponding axis. As a result we obtain a new
independent
unit - mass. It is possible to accept: a kg., a pound, etc. By means of
four dimensions we can describe any body, its form, its disposition in
space and the disposition as to other objects.
Algorithm is
observed.
In
order to describe substance which is characterised by density, let's
draw a corresponding axis. As a result we obtain a new
independent
unit - mass. It is possible to accept: a kg., a pound, etc. By means of
four dimensions we can describe any body, its form, its disposition in
space and the disposition as to other objects.
Algorithm is
observed.
It
is actually the fourth dimension. Properties of substance:
state
of
aggregation of matter ( for
example: gas,
liquid), atomic
structure,etc. is presented in Chemistry.
Let's proceed and create the
fifth dimension.
e) fifth dimension
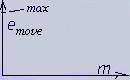 According
to algorithm it must be the product of
mass… into
what? As substance can move then obviously into the unit of
motion. We know that generally accepted unit in this case is velocity.
But it doesn't correspond to our algorithm because velocity is
derivative quantity V= s/t. That's why let's temporarily take
the
existence of an abstract
unit
of motion as
a fact. As motion is always
directed then this unit has a vector. Let's denote it
According
to algorithm it must be the product of
mass… into
what? As substance can move then obviously into the unit of
motion. We know that generally accepted unit in this case is velocity.
But it doesn't correspond to our algorithm because velocity is
derivative quantity V= s/t. That's why let's temporarily take
the
existence of an abstract
unit
of motion as
a fact. As motion is always
directed then this unit has a vector. Let's denote it 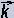 .
We know that maximum velocity of substance motion is velocity
of
light in vacuum. It means that our unit (
.
We know that maximum velocity of substance motion is velocity
of
light in vacuum. It means that our unit (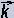 )
must have limit , but it doesn't correspond to our
algorithm.
Have we come into the deadlock? Not at all. If we
take it not as a
dimensional unit but as a coefficient then everything will be put in
order. Let's name this unit - a coefficient
of
processes intensity.We
can take maximal value of a coefficient = 1 or for convenience =
300thousand (meaning the velocity of light is 300.000km/sec),
it
's not important, the
matter is this coefficient can
describe any motion without ambiguity.
)
must have limit , but it doesn't correspond to our
algorithm.
Have we come into the deadlock? Not at all. If we
take it not as a
dimensional unit but as a coefficient then everything will be put in
order. Let's name this unit - a coefficient
of
processes intensity.We
can take maximal value of a coefficient = 1 or for convenience =
300thousand (meaning the velocity of light is 300.000km/sec),
it
's not important, the
matter is this coefficient can
describe any motion without ambiguity.
For example, (Kmax = Klight): a car moves at the speed of
100km/hour - the coefficient here = 0.027, and the speed of
the
rocket = 2000km/hour, here the coefficient = 0.55 and so
on. You
aren't accustomed to it yet? But it's correct.
You'll make sure of it in the further account.
Product of mass into a vector coefficient gives a new independent unit
of
dimension. Let' denote it 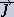 . The dimension range
is positive numbers from 0 to ∞.
How shall we call it? The correct name can be a pulse, but
this term
exists already. Our unit has quite different meaning, that's
why let's
name it vector
mass (
. The dimension range
is positive numbers from 0 to ∞.
How shall we call it? The correct name can be a pulse, but
this term
exists already. Our unit has quite different meaning, that's
why let's
name it vector
mass ( ).
).
In fifth dimension rectilinear
motion of a
body or several bodies , their possible interaction (
everything is going on in one line) is described.
We are on
the boundary between classic and quantum physics and have
entered the area of vector algebra. Algorithm of
dimensions' construction has been observed, we can start with a new
dimension.
(By the way, those who would like to travel in 'other' dimensions, the
fifth one suits here well: make some steps - and you
are there).
f) sixth dimension
 Substance
can move not only along a strait line but also in the plane.You'll get
convinced in it when you pour some water on any surface. We'll create
the
required dimension for describing such processes. I think
it's
not necessary to explain what axis should be added. As a
result
we get a new independent unit which equals the
product
Substance
can move not only along a strait line but also in the plane.You'll get
convinced in it when you pour some water on any surface. We'll create
the
required dimension for describing such processes. I think
it's
not necessary to explain what axis should be added. As a
result
we get a new independent unit which equals the
product  ×
× .
As you can see this is the product of two vectors.
Sorry,
but let me remind you: in vector algebra there are
two
multiplications:
.
As you can see this is the product of two vectors.
Sorry,
but let me remind you: in vector algebra there are
two
multiplications:
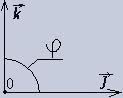
 The first one is scalar ?×b×cosφ,
as φ=90?,
in this case the product equals -0. We aren't going to
examine this version here, bit it should be pointed out that
this
formula is the basis for the unified field theory. We can discuss it if
you
'd like to.
The first one is scalar ?×b×cosφ,
as φ=90?,
in this case the product equals -0. We aren't going to
examine this version here, bit it should be pointed out that
this
formula is the basis for the unified field theory. We can discuss it if
you
'd like to.
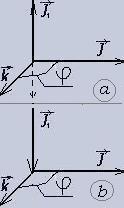
The second
is the vector product. This is a new vector with scalar
quantity which equals a×b×sinφ, we have k×i×sin90?
i.e.
i1 =
k×i.
But its direction is perpendicular to the plane of co-ordinates .
Moreover, this vector is non-commutative. Simply speaking, it can be
directed to both sides. (fig.a). What does it mean? I am going to
explain it but at first let's transform this figure.
Let's
take one of two possible vectors - the lower one at
first. According to the rules of vector algebra we can
carry
vector (preserving it being parallel). See figure b.
We have already mentioned a jet of water falling down on the
plane.
Here we
describe similar processes. The jet, when falling down, spread
out at the angle of φ =
360°,
but if we pour it in the corner of the room it will spread
out at
the angle of 90°. Similar processes take
place if
we take the second vector. Let's direct a jet of water up from a hose
(ignoring Earth's gravitation) .It concerns non-commutativity.
Please pay attention to the fact how clear the regularity of
dimension's presenting in the form of one axis is exhibited
here.
We have created the next dimension, algorithm has been observed,but we
can't see a new unit of dimension. In fact multiplying
quantity
by a coefficient we will not get a new unit . But multiplying this
quantity by a vector
coefficient we get a new unit. This unit has different direction of a
vector. So algorithm has been observed. Here
mathematics
is vector algebra and everything that we used
before.
( Travelling in this
dimension is possible, but very undesirable).
g) seventh dimension
Substance can move not only along the straight line or in the plane but
also in the volume: sound, light,
explosion and so on.
It's not necessary to describe the construction of this dimension , it
is similar to the preceding dimension.
Let's talk of NEST-DOLLS. The last three dimensions exhibit
this
phenomenon explicitly: substance when moving "finds"
necessary
dimension itself depending on conditions. For example, a flying
stone as it struck the wall scatters - goes from fifth to sixth
dimension. Water running down by a hole from the surface -
goes
from sixth to fifth dimension,
a gun shot - goes from seventh to fifth dimension, and a mere
explosion - goes from fourth to seventh
dimension and
so on.
Now let me explain what sinφ
is. Shortly speaking this sinφ
forms wave gist in any motion.You can ask me a question: what
about rectilinear motion? Let's use vector
mathematics
here. You know that two and more vectors in the plane or in
space
can be converged into one vector by means of adding together.
But
we can present one vector in the form of two or three ones.
Thus rectilinear motion is a particular case of
motion.
So the attempt to
explain "the fourth
dimension" has brought us to the creation of a certain
system.
This system permits us
to answer many questions.
Some additional information and
examples
The beginning of a page
To the
title-page  Send a message, please
Send a message, please 
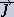 ).
). 


 and can be named : a litre,a gallon,
etc. The obtained unit is independent.
With the help of the third dimension we can
describe solid figures, spatial
lines and their
mutual disposition. Here mathematics
is stereometry, algebra,
differential calculation.
and can be named : a litre,a gallon,
etc. The obtained unit is independent.
With the help of the third dimension we can
describe solid figures, spatial
lines and their
mutual disposition. Here mathematics
is stereometry, algebra,
differential calculation.  Three
dimensions are depicted in fig.4. In order to construct fourth
dimension one more axis should be drawn. Drawing it
in the
domain of these three dimensions doesn't have any sense. And
drawing it in the domain of negative numbers contradicts to algorithm.
It should be noted that Decart system of
co-ordinates (
axes at angle 90˚ ) isn't a dogma. For example, axes can have 60˚ as it
is shown in fig.5. To draw here the fourth axis seems quite possible .
Please try if you've got time. One needs to understand that
all
the dimensions are abstraction, created by ourselves for
describing something. There is objective reality: space, material
bodies, processes occurring in substance. We
have described space in
three
dimensions, it's time to describe substance.
Three
dimensions are depicted in fig.4. In order to construct fourth
dimension one more axis should be drawn. Drawing it
in the
domain of these three dimensions doesn't have any sense. And
drawing it in the domain of negative numbers contradicts to algorithm.
It should be noted that Decart system of
co-ordinates (
axes at angle 90˚ ) isn't a dogma. For example, axes can have 60˚ as it
is shown in fig.5. To draw here the fourth axis seems quite possible .
Please try if you've got time. One needs to understand that
all
the dimensions are abstraction, created by ourselves for
describing something. There is objective reality: space, material
bodies, processes occurring in substance. We
have described space in
three
dimensions, it's time to describe substance. Here the unit
is - an agreed piece.
Here the unit
is - an agreed piece. It can be represented in the form of one axis,
because
this dimension has already included the previous
one. Here
the unit of measure is an agreed
area.
It can be represented in the form of one axis,
because
this dimension has already included the previous
one. Here
the unit of measure is an agreed
area.  It can also be represented
in the form of one axis. Here the unit of measure is an agreed cubic
content.
It can also be represented
in the form of one axis. Here the unit of measure is an agreed cubic
content.  In
order to describe substance which is characterised by density, let's
draw a corresponding axis. As a result we obtain a new
independent
unit - mass. It is possible to accept: a kg., a pound, etc. By means of
four dimensions we can describe any body, its form, its disposition in
space and the disposition as to other objects.
Algorithm is
observed.
In
order to describe substance which is characterised by density, let's
draw a corresponding axis. As a result we obtain a new
independent
unit - mass. It is possible to accept: a kg., a pound, etc. By means of
four dimensions we can describe any body, its form, its disposition in
space and the disposition as to other objects.
Algorithm is
observed. According
to algorithm it must be the product of
mass… into
what? As substance can move then obviously into the unit of
motion. We know that generally accepted unit in this case is velocity.
But it doesn't correspond to our algorithm because velocity is
derivative quantity V= s/t. That's why let's temporarily take
the
existence of an abstract
unit
of motion as
a fact. As motion is always
directed then this unit has a vector. Let's denote it
According
to algorithm it must be the product of
mass… into
what? As substance can move then obviously into the unit of
motion. We know that generally accepted unit in this case is velocity.
But it doesn't correspond to our algorithm because velocity is
derivative quantity V= s/t. That's why let's temporarily take
the
existence of an abstract
unit
of motion as
a fact. As motion is always
directed then this unit has a vector. Let's denote it  .
We know that maximum velocity of substance motion is velocity
of
light in vacuum. It means that our unit (
.
We know that maximum velocity of substance motion is velocity
of
light in vacuum. It means that our unit (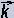 )
must have limit , but it doesn't correspond to our
algorithm.
Have we come into the deadlock? Not at all. If we
take it not as a
dimensional unit but as a coefficient then everything will be put in
order. Let's name this unit - a coefficient
of
processes intensity.We
can take maximal value of a coefficient = 1 or for convenience =
300thousand (meaning the velocity of light is 300.000km/sec),
it
's not important, the
matter is this coefficient can
describe any motion without ambiguity.
)
must have limit , but it doesn't correspond to our
algorithm.
Have we come into the deadlock? Not at all. If we
take it not as a
dimensional unit but as a coefficient then everything will be put in
order. Let's name this unit - a coefficient
of
processes intensity.We
can take maximal value of a coefficient = 1 or for convenience =
300thousand (meaning the velocity of light is 300.000km/sec),
it
's not important, the
matter is this coefficient can
describe any motion without ambiguity.
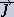 . The dimension range
is positive numbers from 0 to ∞.
How shall we call it? The correct name can be a pulse, but
this term
exists already. Our unit has quite different meaning, that's
why let's
name it vector
mass (
. The dimension range
is positive numbers from 0 to ∞.
How shall we call it? The correct name can be a pulse, but
this term
exists already. Our unit has quite different meaning, that's
why let's
name it vector
mass (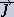 ).
).  Substance
can move not only along a strait line but also in the plane.You'll get
convinced in it when you pour some water on any surface. We'll create
the
required dimension for describing such processes. I think
it's
not necessary to explain what axis should be added. As a
result
we get a new independent unit which equals the
product
Substance
can move not only along a strait line but also in the plane.You'll get
convinced in it when you pour some water on any surface. We'll create
the
required dimension for describing such processes. I think
it's
not necessary to explain what axis should be added. As a
result
we get a new independent unit which equals the
product 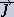 ×
×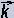 .
As you can see this is the product of two vectors.
Sorry,
but let me remind you: in vector algebra there are
two
multiplications:
.
As you can see this is the product of two vectors.
Sorry,
but let me remind you: in vector algebra there are
two
multiplications: The first one is scalar ?×b×cosφ,
as φ=90?,
in this case the product equals -0. We aren't going to
examine this version here, bit it should be pointed out that
this
formula is the basis for the unified field theory. We can discuss it if
you
'd like to.
The first one is scalar ?×b×cosφ,
as φ=90?,
in this case the product equals -0. We aren't going to
examine this version here, bit it should be pointed out that
this
formula is the basis for the unified field theory. We can discuss it if
you
'd like to. Send a message, please
Send a message, please 